Cannonball Aerodynamic Drag
Abstract
This article gives a brief discussion of the aerodynamics of smooth spheres, cannonball size, travelling near the speed of sound and develops a model of drag coefficient as a function of velocity and sphere diameter.
Historical Background
Newton's experiments to determine the nature of fluid resistance formed the basis of Book II of his famous "Principia", Newton contended that fluid resistance is proportional to the square of the object's speed through the fluid, the spherical body's cross-sectional area and the density of the medium. Hence the drag force may be formulated by the equation: $$ F = \frac{1}{2} C_D \rho A v^2 \tag{1} $$
where:
\(C_D\) is the non-dimensional drag coefficient,
\(\rho\) is the fluid density,
\(A\) is the cross-sectional area of the object, and
\(v\) is the velocity of the body through the fluid.
Newton experiments yielded the first accurate measurements of fluid drag forces. He measured the drag coefficient of a sphere to be 0.5, in good agreement with currently accepted value of 0.44 to 0.47 for low speed drag on a smooth sphere.
The invention of the ballistic pendulum in the early 1740s by Benjamin Robins provided the first means of accurately measuring the speed of very high speed spheres, i.e. round shot fired from guns. Robins' measurements showed an increase in drag by as much as a factor of 3 for high speed bullets compared to that predicted by a constant CD = 0.5. This may be best modelled by assuming CD varies as a function of speed, and provides a correction to the drag's predominant v2 dependence.
Since the ballistic pendulum stopped the projectile to measure its speed, it was restricted to only one velocity measurement per shot. Significant shot to shot variation from smooth bore guns limited the accuracy of deceleration measurements using this technique.
The invention of the chronograph by Francis Bashforth in the 1850's solved this problem by allowing as many a 10 velocity measurements, at widely separated distances, to be made on a single shot. Bashforth measured the deceleration of different projectile shapes and sizes over a wide range of speeds.
Bashforth's experiments were made at a time when the use of artillery firing round shot was rapidly declining in favour of ogive shaped cylindrical bullets. Later ballistic measurements all but ignore round shot, so Bashforth's measurements are among the only measurements made on high speed, cannonball sized spheres.
The original Bashforth experimental data were among those examined by Miller and Bailey in their 1979 paper [2] which summarised the available experimental measurements of aerodynamic drag on spheres travelling at speeds near the speed of sound. It transpires that the combination of speed, size and shape of cannonballs puts their motion in a very interesting region of fluid dynamic behaviour, one where the drag cannot readily be modelled on a single ballistic table and then scaled according to mass and diameter. The following drag coefficient model for round shot is based on the experimental data presented in the Miller and Bailey paper.
Fluid Dynamics of Spherical Projectiles
The aerodynamic drag force on a projectile is governed by two major influences. The first relates to the work required to move the air flow out of the projectile's path which depends of the density and viscosity of the air and the speed and size of the projectile. These effects are incorporated into a dimensionless quantity called the Reynolds number, Re, given by the expression $$ R_e = \frac{vd\rho}{\eta} \tag{2} $$
where:
\(v\) is the velocity of the projectile
\(d\) is the diameter of the cross section of the projectile
\(\rho\) is the density of air, and
\(\eta\) is the viscosity of air.
The value of the Reynolds number for a situation described by these variables will indicate the type of flow that can be expected; turbulent, laminar, vortex shedding etc.
Fig 1 shows the drag coefficient for a sphere travelling through air, at speeds well below the speed of sound, as a function of the Reynolds number.
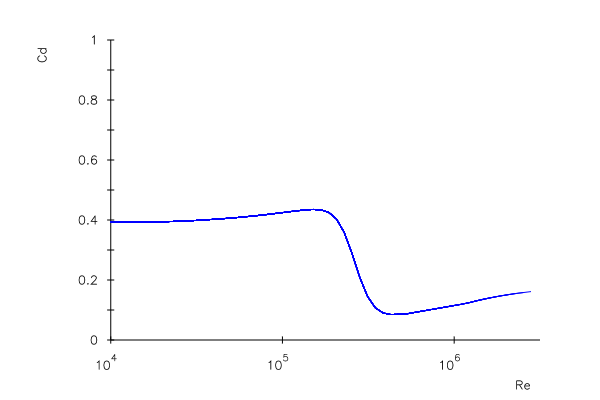
Figure 1. Drag coefficient for spheres as a function of Reynolds number [after Morrison]. The function plotted is SphereDragVsRe(Re) source code presented below.
Fig 1. shows that at low Reynolds numbers, spheres exhibit a roughly constant drag with a CD value ~0.47, and at higher Reynolds numbers they exhibit CD values from 0.1 to 0.2. The decrease in drag occurs for Reynolds numbers greater than ~400,000 indicates an abrupt change from separated laminar to separated turbulent flow. Turbulent flow separates from the sphere's surface later than laminar flow, so the area of low pressure behind the sphere is smaller, reducing net drag. There is a description and animation of this effect on the NASA website.
The second major influence in high speed drag is the pressure increase due to the build-up of shock waves ahead of a projectile when its speed is close the speed of sound. The ratio of projectile speed to the speed of sound is termed the Mach number.
Drag Near the Speed of Sound
The speed range of interest for smooth bore guns is from ~100 m/sec to ~700 m/sec, since the speed of sound is ~340 m/sec, this corresponds to a range of Mach numbers from 0.3 to 2.0, so the additional forces associated with projectiles travelling near the speed of sound will be significant.
Fig 2 shows a plot of the drag coefficient as a function of Mach number for spheres ranging in diameter from 2.5 mm to 12.5 mm. The curve is a manual fit to chronograph data [Miller & Bailey, 1979]. The rapid increase in drag as a function of Mach number at velocities near the speed of sound is clear.

Figure 2. Small sphere drag coefficient as a function of Mach number.
Small diameter spheres, even travelling at speeds up to 700 m/sec (Mach 2) have Reynolds numbers below 5×105, the critical Reynolds number. It can be seen from Fig 1, that the flow regime below this critical Reynolds number remains roughly constant. This means that small arms bullets of different diameters and speeds will all behave in a similar manner. Hence, the drag on a standard spherical bullet can be measured in detail and the drag expected for other spherical bullets will simply scale with the cross-sectional area and inversely with its mass. This is the basis on which the GS Ballistic tables, which are based on drag measurements on a 'standard' spherical bullet, 9/16" diameter.
The cast-iron cannonballs used up until the mid 1800s ranged in size from ~50 mm (2") diameter with mass of ~1 lb, up to ~190 mm (7.5") diameter which have mass ~64 lb. The range of speeds at which these cannonballs travelled was from a muzzle velocity of ~700 m/sec, to a terminal velocity of ~100 m/sec, so the Reynolds numbers will range from 8×106 down to 3×105.
This range of Reynolds numbers straddles the critical value where the sharp drop in drag occurs. The speed range also straddles the sound speed, where a rapid increase in drag as a function of projectile speed occurs. So rapid changes in the drag coefficient value can be expected. Miller and Bailey's analysis of the accumulated drag data for spheres travelling at these speeds is summarised in Fig 3.
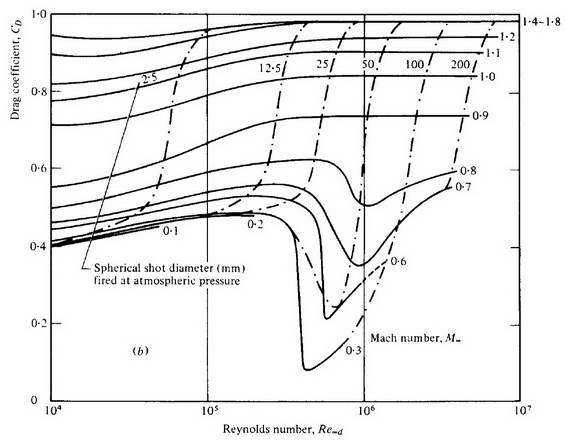
Figure 3. Drag coefficient of spheres as a function of Reynolds number for various Mach number values (from Miller & Bailey 1979).
The solid lines are graphs of the coefficient of drag as a function of Reynolds number for different Mach number values. The drag for the whole range of Reynolds numbers clearly rises as the Mach number increases as has been discussed above. The dashed curves plot the drag coefficient values for different sized spheres (diameters are shown in mm). For the small diameter spheres (2.5 to 25 mm) the drag shows the characteristic increase with rising Mach numbers as seen in Fig 2.
For the various larger diameter spheres it is clear that drag coefficient values as a function of speed (or Reynolds number) are very different. The plot of the drag coefficient for the 50 mm diameter spheres is complex, with a drop in drag with increasing Reynolds number followed by a rapid increase as the flow speed crosses the sound speed (Mach 1.0).
This effect may be seen more clearly if by plotting the drag coefficient for different size smooth spheres, as a function of Mach number.
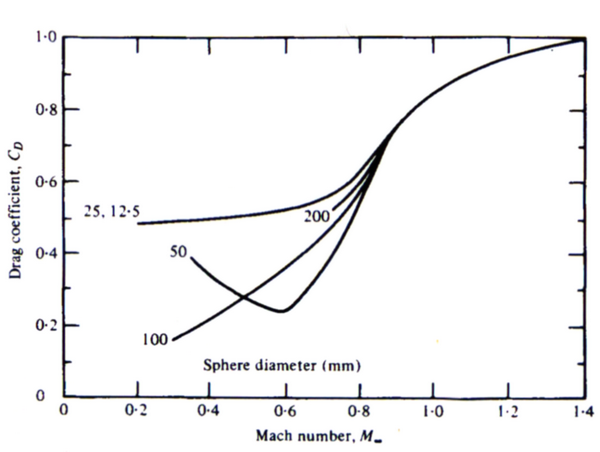
Figure 4. Drag coefficient as a function of Mach number for various diameter spheres.
The shape of the drag curves in Fig 4 is the combination of the two effects described above, flow regime change near the critical Reynolds number causing a drop in drag with increasing Mach number, and the increase in drag due to shock wave build-up near the speed of sound. The drag curve for small spheres is below the critical Reynolds number for Mach numbers plotted, so the drag curve just exhibits the increase near the sound speed as seen in Fig 2. For sphere diameters of 50 mm, at higher speeds the Reynolds number increases with the rapid drop in drag above the critical value occurring around Mach 0.5. Above Mach 0.5 the drag is very much less than the drag small spheres experience at this speed. For speeds above Mach 0.6, the additional drag due to the shock wave formation comes into play and the drag coefficient value rises to ~1, just as for small spheres. For sphere diameters 100mm or greater, the flow regime stays above the critical Reynolds number for a wider range of Mach numbers. The drag for the larger spheres remains around 0.2 for subsonic Mach numbers this would apply at the sphere's terminal velocity which is as low in speed as ballistic measurements are concerned, but at very slow speeds, the drag would rise to the familiar 0.4 to 0.5 as the Reynolds number drops to sub-critical values.
Modelling Cannonball Aerodynamic Drag
To model the behaviour of drag coefficient for spheres travelling at speeds near Mach 1, the drag due to the effect of shock wave build-up is superimposed on the drag behaviour due to critical Reynolds number effects. A function, denoted k(Mn), which smoothly rises in value from 0 at Mach 0.2 to 1 at Mach 1.4 is a good model for the shock formation drag. This is added to the normal drag, varying with Reynolds number (shown in Fig 1). The shock wave drag dominates the flow regime near the speed of sound, which can be modelled by multiplying the Reynolds drag by a masking function, t(Mn), which falls from 1 at Mach 0.3 to 0 at Mach 1.1. The other effect that needs to be modelled is the movement of the critical Reynolds number from its normal value of 470,000 to values above 1,000,000 for supersonic flow regimes. Sliding the critical Reynolds number to higher Reynolds numbers is achieved by scaling the value passed to the SphereDragVsRe function (plotted in Fig 1). The scale function, denoted s(Mn), is 1 for low Mach numbers then drops down to 0.5 at Mach 1.
The resulting expression for the drag coefficient is given by, $$ C_D = k(Mn) + f(Mn)*SphereDragVsRe(s*Re). $$ The expressions for \(k(Mn), t(Mn), s(Mn)\) are combined in the function \(SphereDrag(v, d)\) taking as parameters the instantaneous velocity, v, and the sphere diameter, d. Hence the drag coefficient for large spheres in the speed range Mach 0.2 to 2.0 is given by $$ C_D = SphereDrag(v, d). $$
The output from these relatively simple functions modelling the fluid dynamic effects is shown in Fig 5, which the graph of the drag coefficient as a function of Reynolds number for several Mach numbers. These graphs may be compared to the Miller & Bailey curves fitted to the experimental data shown in Fig 3.
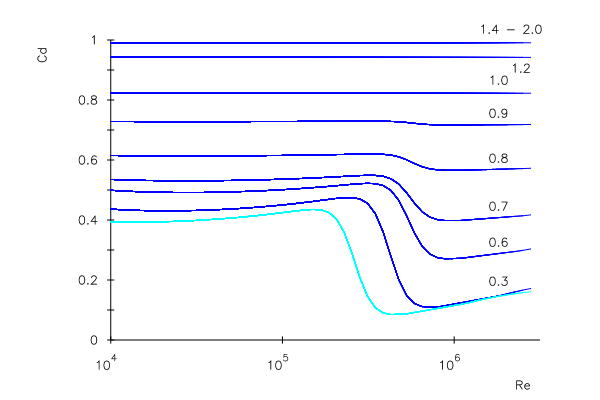
Figure 5. Predicted drag coefficient as a function of Reynolds number for various Mach numbers. Light blue curve is low Mach number plot from Fig 1.
Plotting the resulting drag coefficient values as a function of Mach number for various diameter spheres, generates the drag coefficient graphs shown in Fig 6. These may be compared to the Miller & Bailey curves fitted to the experimental data shown in Fig 4.
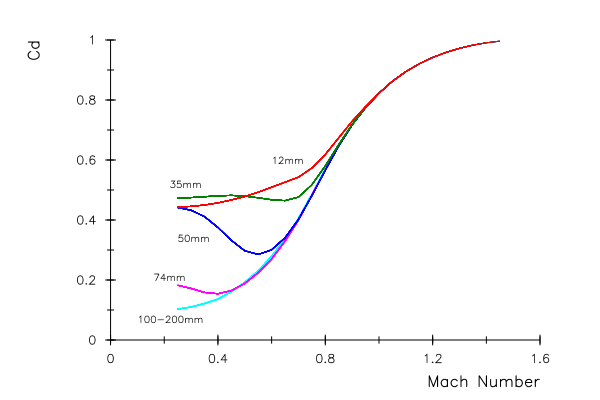
Figure 6. Predicted drag coefficient as a function of Mach number for various diameter spheres.
Notes on Mathematical Methods
The three functions, \( k(Mn), t(Mn) \) and \( s(Mn) \) used to model the fluid dynamics all have a basic \( atan \) shape. The function \( s(Mn) \) is symmetric and is expressed as a simple \( atan \) function, $$ s(Mn) = 0.78+0.22 \; atan(-12 (Mn-0.23)) $$ The \( k(Mn) \) and \( t(Mn) \) functions are not symmetric and were modelled with a cubic Bezier function. The Bezier control points were adjusted to get a good fit to the experimental data.
If the 4 control points are \( (P0.x,P0.y), \: (P1.x,P1.y), \: (P2.x,P2.y) \) and \( (P3.x,P3.y) \). The general cubic Bezier, in parametric form, is given by: $$\begin{aligned} x(u) &= P0.x\; ( 1 - u )^3 + P1.x\; 3 u ( 1 - u )^2 + P2.x\; 3 u^2 ( 1 - u ) + P3.x\; u^3 \\ y(u) &= P0.y\; ( 1 - u )^3 + P1.y\; 3 u ( 1 - u )^2 + P2.y\; 3 u^2 ( 1 - u ) + P3.y\; u^3 \end{aligned}$$ where \( u \) varies from \( 0 \) to \( 1 \).
In this notation, the Mach number, \( Mn \), is the \( x \) variable and the drag coefficient, \( Cd \), is the \( y \) variable.
The 4 control points for \( k(Mn) \) are: $$ P0 = (0.1, 0.0), P1 = (0.95, 0.0), P2 = (0.55, 0.95), P3 = (1.5, 1.0). $$ The 4 control points for \( t(Mn) \) are: $$ P0 = (0.0, 1.1), P1 = (0.85, 1.1), P2 = (0.57, 0.05), P3 = (1.0, 0.0). $$
The parametric form of the Bezier equations prevents direct substitution of an \( x \) value to return a \( y \) value. To overcome this problem and still use the simple form of the Bezier functions, a Bezier value finder function, bezier4pt has been provided. This uses de Casteljau's algorithm to recursively find the point of the Bezier curve as close as desired to the target \( x \) value and returns the corresponding \( y \) value. The bezier4pt function only works on cubic Bezier functions that are single valued for all \( x \) in the range. The source code for bezier4pt is included in the listing below.
Software Listing
/*================================================================
SphereDrag
Calculation of aerodynamic drag coefficient for a sphere at
speeds near the speed of sound.
Free to use. Please give credit to A.R.Collins [www.arc.id.au]
last rev: 08Mar16
================================================================*/
/*---------------------------------------------------------------
bezier4pt() finds approximate y from cubic Bezier given x
worst case y(x + xerr) is returned (where xerr is optional parm)
assumes fn is well behaved ie single valued for all x
Adapted from [http://antigrain.com/research/adaptive_bezier/]
*/
function bezier4pt(x, x1, y1, x2, y2, x3, y3, x4, y4, dx)
{
// Calculate mid-points of line segments
var x12 = (x1 + x2) / 2,
y12 = (y1 + y2) / 2,
x23 = (x2 + x3) / 2,
y23 = (y2 + y3) / 2,
x34 = (x3 + x4) / 2,
y34 = (y3 + y4) / 2,
x123 = (x12 + x23) / 2,
y123 = (y12 + y23) / 2,
x234 = (x23 + x34) / 2,
y234 = (y23 + y34) / 2,
x1234 = (x123 + x234) / 2,
y1234 = (y123 + y234) / 2,
xerr = dx || 0.0005; // acceptable x error
if (x<=x1)
{
return y1;
}
if (x>=x4)
{
return y4;
}
// x1234, y1234 is on the curve and between x1 and x4
if (x>=x1234) // x is on new shorter curve between x1234 and x4
{
if ((x-x1234) > xerr)
{
return bezier4pt(x, x1234, y1234, x234, y234, x34, y34, x4, y4);
}
else
{
return y1234;
}
}
else // x is on new shorter curve between x1 and x1234
{
if ((x1234-x) > xerr)
{
return bezier4pt(x, x1, y1, x12, y12, x123, y123, x1234, y1234);
}
else
{
return y1234;
}
}
}
/*---------------------------------------------------------------
SphereDragVsRe() returns Reynolds number for flow past a sphere
from "Data Correlation for Drag Coeff for Sphere" F.A.Morrison
[chem.mtu.edu]
*/
function SphereDragVsRe(Re)
{
var Cd;
function log10(val)
{
return Math.log(val) / Math.log(10);
}
if (Re > 2E6)
{
Cd = 0.15;
}
if (Re > 1.2E6)
{
Cd = 0.19 - 8E4/Re;
}
else if (Re > 4.77E5)
{
Cd = -0.485 + 0.1*log10(Re);
}
else
{
Cd = 24/Re + (2.6*(Re/5))/(1+Math.pow(Re/5,1.52)) + \
(0.411*Math.pow(Re/263000,-7.94))/(1+Math.pow(Re/263000,-8)) + Math.pow(Re,0.8)/461000;
}
return Cd;
}
/*---------------------------------------------------------------
SphereDrag() modifies Morrison drag coeff v Reynolds number for
speeds near Mach 1 to match experiment data summarised in
'Sphere Drag at Mach Numbers from 0.3 to 2.0'
Miller & Bailey [J.Fluid Mech, 1979].
*/
SphereDrag = function(v, d) // speed, diameter
{
// Imperial units
var SSpd = 1116, // sound speed at sea level (340.2 m/s)
rho = 0.074, // density of air (1.225 kg/m^3)
eta = 3.75E-7, // viscosity of air (1.81E-5 kg/m.s)
Mn = v/SSpd, // Mach number
Re, k, t, sf,
Cd;
if (Mn<0.2)
{
Mn = 0.2;
}
if (Mn>1.5)
{
Mn = 1.5;
}
Re = v*d*rho/eta; // Reynolds number
k = (Mn>=1.5)? 1.0: bezier4pt(Mn, 0.1, 0.00, 0.95, 0.0, 0.55, 0.95, 1.5, 1.0);
t = (Mn>1.0)? 0.0: bezier4pt(Mn, 0.0, 1.1, 0.85, 1.1, 0.57, 0.05, 1.0, 0.0);
sf = 0.78+0.22*Math.atan(-12*(Mn-0.23));
Cd = k + t*SphereDragVsRe(sf*Re);
return Cd;
};
References:
1. F.A. Morrison, www.chem.mtu.edu/~fmorriso/DataCorrelationForSphereDrag2010.pdf 2010.
2. D.G. Miller & A.B. Bailey, Sphere Drag at Mach Numbers from 0.3 to 2.0 1979.
3. M. Shemanarev http://antigrain.com/research/adaptive_bezier/