UNDERWATER SOUND PROPAGATION

Temperature and Sound Velocity Profiles

In the ocean the speed of sound C, is a function of temperature pressure and salinity. Eqn (1) shows the dependence of sound speed on these factors:

$C(T, P, S) = 1449.2 + 4.6\ T + 0.055\ T^2 + 1.39\ (S - 35) + 0.016\ D \qquad (1)$ $C\ \mbox{in m/sec.}\ T\ \mbox{in deg Celcius,}\ D\ \mbox{in metres and}\ S\ \mbox{in parts per thousand.}$

In the oceans salinity, S, is about 35ppt, and so the sound speed formula reduces to a function of temperature and depth.

From Eqn 1 it can be seen that the sound speed is strongly dependant on the water temperature T. Solar radiation warms the surface of the ocean, wave action tends to mix the hot surface layer with the cooler lower layers generating a surface layer of fairly uniform temperature. In temperate and tropical waters this isothermal surface layer may extend from 20m to 200m deep. The water temperature below this layer rapidly drops away. This region of falling temperature is called a negative thermocline.

The ocean depths, where little or no sunlight penetrates is of uniform temperature, only 1 or 2°C above freezing. In these isothermal regions, the sound speed, C, increases with depth due to the pressure. The rate of increase is 0.016 m/sec/m.

Figure 1. Typical Eastern Pacific winter bathythermograph

Fig 1 shows a plot of temperature as a function of water depth, a bathythermograph, for the 500m near the surface. This bathy's mixed layer and thermocline are clearly defined and are typical of warmer ocean regions.

The isothermal layer extends down to 60m. The temperature in this layer is 17°C.

Fig 2 shows the corresponding sound speed profile. At the sea surface the sound speed is about 1512 m/sec while at 60m the sound speed has risen to about 1513 m/sec due to the increased depth. The sound speed then rapidly falls for the lower temperature, deeper layers.

Figure 2. Sound velocity profile corresponding to the bathy shown in Fig 1.

In colder waters with less solar radiation results in small or no isothermal surface layer. The temperature continuously declines with depth from the surface.

The sound profile of Fig 4 is typical of high latitudes where heating from solar radiation is not so significant. This marked differences in acoustic conditions in different locales indicate that sonar conditions in one area may not be applicable to another area or season.

Knowledge of the temperature profile and hence the sound speed profile, enables the prediction of sound transmission paths. Such information serves as input to the tactical environment in which submarine and surface navies operate.

Figure 3. Bathy with no isothermal surface layer.

Figure 4. Sound speed profile corresponding to the bathythermograph of Fig 3.

Ships employ Expendable Bathythermographs (XBT) to measure the water temperature as a function of depth. These probes sink at a known rate. The temperature measurements are sent back to the ship's receiver via a fine copper cable unreeling from the probe and are logged or displayed (on an appropriate scale) as sound speed versus depth.

Submarines use a similar device, the SSXBT, which is ejected from the dived submarine, floats to the surface and then sinks at a known rate.

Sound Ray Tracing

The propagation paths of sound in the ocean may predicted using much the same techniques employed to predict the reflection and refraction of light rays.

In crossing the interface between the different media, such as from air to glass, the light ray is refracted or bent. The angle of refraction depends on the ratio of the speed of light in the two media, this is Snells law. A similar process occurs with sound transmission in the ocean.

For calculating the ray paths, the ocean may be considered as a set of thin layers of water of different sound speeds.

Fig 5 illustrates Snells Law for refraction of sound rays.

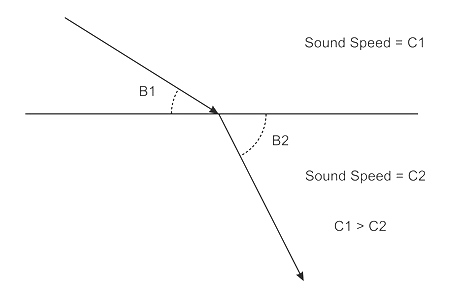
Figure 5. Diagram of the refraction of sound rays.

Referring to Fig 5, Snells law for sound in water may be stated as:

$\frac{\cos(B_1)}{\cos(B_2)} = \frac{C_1}{C_2} \qquad (2)$

Hence, if the angle of a ray to the horizontal is B₁, in a region of sound speed C₁, then the refracted ray angle, B₂ as it passes into region with sound speed C₂ can be calculated.

From Eqn 2, if C₁>C₂ then cos(B₁)>cos(B₂) and hence B₁<B₂, i.e. for a ray passing into a slower sound speed layer, the ray angle is larger, it bends away from the horizontal. Conversely, if C_l<C₂ then B_l>B₂ and the ray is shallower, nearer to horizontal. When the sound speed increases the ray angle tends to decrease.

Snells law may be restated for acoustic rays: "sound rays passing from one medium to another bend toward the medium with the slower wave speed"

If a bathy has been taken, the sound speed C as a function of temperature and depth is known and the angles through which sound rays will bend as they pass through different depths can be calculated and the ray paths plotted.

Fig 6 shows some ray paths which may occur for the bathy in Fig 1 (sound speed profile of Fig 2).

Figure 6. Possible ray paths for the bathy in Fig 1.

For a sound source located in the surface duct there is a ray which just becomes horizontal at the bottom of the mixed layer. This ray and all smaller angle rays are trapped in the duct as they don't cross into the negative thermocline.

The launch angle of this critical ray is given by putting B₁ = 0 and hence cos(B₁) = 1 in Eqn (2), and substituting the appropriate values for the sound speed.

$B_2 = \cos^{-1}\left(\frac{C_2}{C_1}\right)$

For a source depth of 5m, a typical depth for a surface ship active sonar, the source angle for rays to be trapped in the duct is given by:

$B_s = \cos^{-1}\left(\frac{1512 + 0.017 \times 5}{1512 + 0.017 \times 60}\right) = 2^\circ$

The same ray angle applies for rays that start in an upwards direction as these are merely reflected at the sea surface and then pass through the source depth at 2° declination. Hence rays that leave the sonar within 2° of horizontal are trapped within the duct (see Fig 6).

It follows that rays which start at steeper angles can penetrate below the layer. A ray that starts with a steeper angle escapes the duct and is immediately refracted downward, towards the slower sound speed region. It follows that there is a region through which rays don't pass, called the SHADOW ZONE. This is the region where a submarine may be relatively invisible to a surface ship active sonar.

Deep Ocean Propagation

Water temperature deep in the oceans is very nearly constant and in such regions the sound speed is dominated by its dependence on depth, sound speed increasing with increasing depth. Rays which escape the duct are initially refracted downward toward the colder water which has a lower sound speed. Depending on the depth of water the sound may hit the sea floor and be reflected back up, but if the water is sufficiently deep, the sound penetrates to depths where the sound speed increases due to increasing depth. The rays begin to bend back toward the slower sound speed at shallower depths without hitting the bottom.

For this REFRACTED transmission mode to occur, the deep water sound speed must at least equal the sound speed at the source. The sound rays starting horizontal near the surface will become horizontal again at this depth and then bend upward toward the slower sound speed layers above. Rays starting out at steeper angles require deeper water with even higher sound speeds to become horizontal and then turn back toward the surface.

Once the sound has been refracted upwards it travels to the source depth where it again encounters higher sound speeds and bends back to the horizontal. The same process can then be repeated.

The higher sea surface temperature, the deeper the water must be for the deep sound speed to equal the surface speed. So in temperate zones this type of transmission can only occur in deep ocean basins. For example, a surface temperature of 27°C which indicates a sound speed of about 1540 m/sec and the equivalent water depth required is about 5000m. Ocean basins are typically 4000m deep so the phenomenon requires cooler surface temperatures.

Fig 7 shows a schematic of this type of propagation.

Figure 7. Deep water sound showing convergence zones.

Fig. 7 shows that the sound loops back to the surface at regular distances of about 40 to 60km, depending on the surface water temperature. The regions of higher sound strength are termed CONVERGENCE ZONES.

In a region where the water depth is too shallow for refracted transmission paths, sound rays will intersect the sea floor and be reflected. More energy is reflected if the sound speed in the bottom material is hard with much faster sound speed than water. A rocky bottom will reflect sound more efficiently than a muddy bottom.

Thus reflection depends on the characteristics of the bottom and is generally frequency sensitive, with the result that energy in higher frequency bands is reflected better than energy at lower frequencies. Nevertheless BOTTOM BOUNCE can be utilized to our advantage,

Fig 8 shows such an application. Energy from a near surface source, a hull mounted active sonar is initially refracted down and intersects the sea floor where it is reflected. Depending on the ray angle this reflected energy may be able to reach a region that could not be ensonified by direct transmission paths, such as the shadow zone. Some active sonars use this mode to achieve this result.

Figure 8. Ray paths using bottom bounce.

If the sound source is below the layer, then a variation of this refracted propagation path may be sustained. This is illustrated by Figure 9. Because the sound speed increases both above and below the source depth, rays become trapped in this deep sound channel. This is known as SOFAR propagation. The acronym being derived from Sound Fixing And Ranging. Propagation over extremely long distances is possible via this mode.

Figure 9. SOFAR propagation for deep launched rays.

Spreading Laws and Propagation Loss

Intensity, I, of sound is a measure of energy flowing across a unit area perpendicular to the direction of propagation. As sound energy travels through the ocean and spreads over a larger volume, the intensity of the sound decreases.

The term TRANSMISSION LOSS describes by how much the level of sound energy has changed in propagating from one point in the ocean to another point. The transmission loss is defined as the ratio of the acoustic intensity at the measuring point or position of interest to the level at some reference position. If the reference is a transmitter the reference position is taken at a distance of 1m from the source (1 yd in the Imperial system). Hence, the transmission or propagation loss at a point P is given by,

$\frac{I_p}{I_{ref}}$

where I_p and I_ref are the respective acoustic intensities at P and at the reference position.

As sound energy travels from the source it spreads out over the surface of a sphere which increases in radius R. For a given amount of energy emitted the Intensity of the sound will be determined by the size of the sphere over which it has spread. At a distance R from the source the Intensity, I is inversely proportional to the surface area of sphere.

$I = \frac{k}{R^2} \qquad \mbox{where}\ k\ \mbox{is again a constant}$

In the case of spherical spreading from a source, a simple transmission loss law emerges.

If R is the distance to the source and the reference level measured 1 metre from the source. The transmission loss is expressed in decibels (dB):

$TL = 20 \log (R)\qquad \mbox{for spherical spreading}$

The source level of sonar transmitters are quoted as the level 1m from the transmitter, for a high power anti-submarine sonar this is typically about 220dB reµPa. This formula for transmission loss due to spherical spreading implies that every time the range doubles, the sound intensity falls by 6dB. So 2m from the source the level is only 214dB and so on. Doubling the range 10 times gives a sound level 60dB down at 1024m, ie. approximately 1km from the source the level has dropped to 160db. At 16km range, the level would be down to 136dB.

Another factor which affects propagation in the ocean is ABSORPTION. Sound energy is dissipated by a lossy interaction with some of the salts in the water. The process is non-linear with the rate of absorption varying roughly as the square of the frequency, as well as being a function of salinity and temperature. A plot of the absorption of sound in sea water according to temperature and frequency are shown in Fig 10.

The effect of the extra absorption loss is to modify the transmission loss equation so that it now becomes;

$TL = 20 \log (R) + aR \qquad\mbox{where}\ a\ \mbox{is the absorption in}\ dB \ \mbox{per metre}$

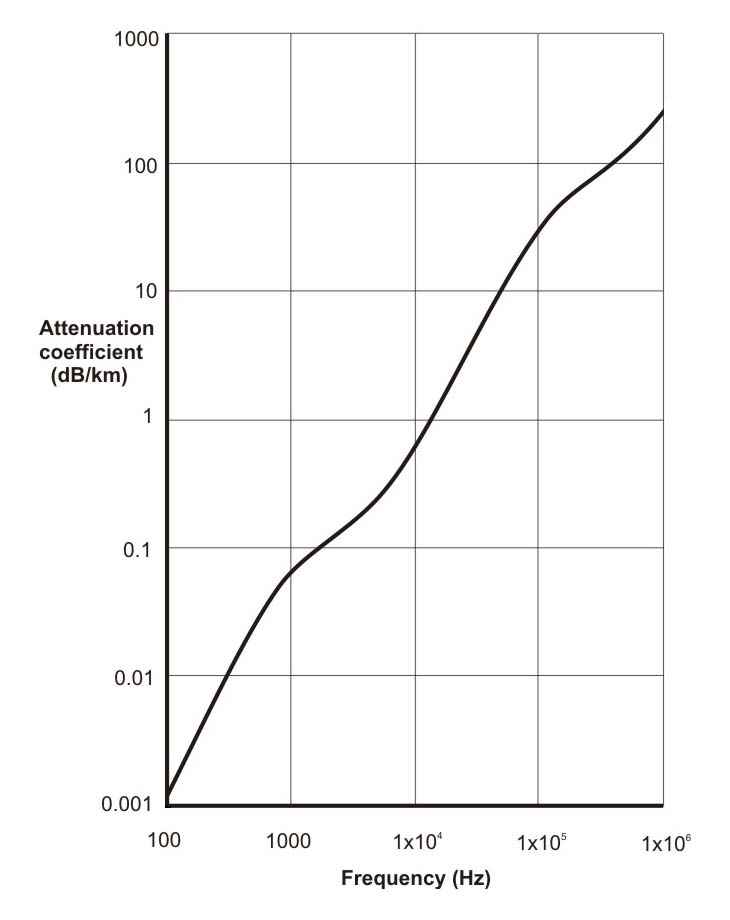
Figure 10. Absorption of sound in sea water (20°C).

The effect of this absorption of sound energy is that the fall in sound pressure level due to spherical spreading is increased by an additional loss for every kilometre the sound travels. This additional absorption loss is small to negligible for frequencies less than 1kHz. But for higher frequency sonars the loss is very significant. For a sonar operating at 15kHz the loss is 2dB per km. So at 16km there will be a 32dB loss in addition to the 84dB spreading loss.